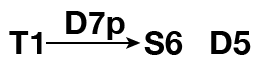Harmonic syntax

Harmonic syntax concerns the norms or principles according to which harmonies (i.e., chords) are placed into meaningful successions. In classical-era Western art music, harmonies generally group into three harmonic functions—tonic (T) or destabilized tonic (Tx), subdominant (S), and dominant (D). Generally speaking, harmonies progress through a cyclical progression of functions:

T → Tx → S → D → T → and so on . . .

However, things are a little more complicated than that when dealing with "real music." Thus, for now, we will limit our study to isolated, complete, self-sufficient phrases. This is an idealized, oversimplified setting—like strict voice-leading—which is useful for learning the basics. Some such phrases even exist in real music! But more often than not, multiple phrases work together to express this complete harmonic progression. However, it is a helpful starting point. Future study will explore how classical composers employ harmonic progressions in larger musical works that combine multiple phrases (which are not self-sufficient) into larger themes and movements.

The idealized phrase

The idealized phrase is a single musical phrase that progresses through an entire cycle of harmonic functions, beginning and ending on tonic. (Strict voice-leading exercises are such phrases.) These phrases begin with a point of stability (tonic), move away from that stable point, and then eventually lead to a point of high tension and resolution (an authentic cadence). This pattern of stability–instability–stability, or rest–motion–rest, with a single goal at the end, should be familiar both from species counterpoint and from strict keyboard-style voice-leading. (This pattern also governs large-scale formal structures in classical music.)

The simplest phrase that exhibits this complete harmonic cycle is:

T1 D5 T1.

This phrase begins and ends with the most stable harmony (T1), and includes an authentic cadence (D5–T1). The D5 is the high point of instability, containing the tendency tone (ti) that most strongly points to the final point of arrival (do, or tonic).

This harmonic cycle can be expanded by inserting a subdominant chord, a destabilized tonic chord, or both, as in the following examples:

T1 S4 D5 T1
T1 Tx6 D5 T1
T1 Tx6 S2 D5 T1

Any harmonic progression that follows the pattern

T1 → (Tx) → (S) → D5 → T1

can serve as the basis for a complete idealized phrase (harmonies in parentheses are optional).

Functional zones

Phrases are seldom 3–5 chords long, however, and functions can be expressed by more than a single chord. Thus we can understand the harmonic functions not simply as chords, but as zones in a phrase, that can be created by a number of chords or short chord progressions. More generally, then, our idealized musical phrase contains a single progression of functional zones T → (Tx) → (S) → D → T, begins with T1, and ends with an authentic cadence (D5–T1).

Triggering and prolonging functional zones

To establish, or trigger, a functional zone, a fixed scale degree must appear in the bass. In other words, tonic can be triggered by T1, subdominant by S2 or S4, and dominant by D5. These are called functional chords (because they trigger the function) or cadential chords (because they can participate in a cadence). Other chords are called contrapuntal chords, and are used to prolong a function throughout the zone. (Note that because Tx is destabilized by nature, it does not take a fixed scale degree in the bass. In fact, Tx almost always appears as Tx6, and it will immediately proceed to S or D.)

Functional prolongations are shown in the functional bass analysis. Such an analysis is called an interpreted functional bass, because the harmonies are interpreted according to the way they behave in the phrase, rather than merely labeled. Generally speaking, parentheses () or curly brackets {} are used to denote prolongation of a function.

Following are the primary techniques used to prolong functional zones in an idealized classical phrase. Examples of specific progressions and notational conventions are provided.

Change-of-figure prolongation

A change-of-figure prolongation occurs when the bass repeats (or is sustained, or drops an octave) while one or more of the upper voices change. If the function and the bass scale degree remain the same, the functional bass remains the same, but the thoroughbass figure changes.

Change-of-bass prolongation

A change-of-bass prolongation occurs when two chords of the same function appear back-to-back, but with different bass pitch classes. D5–D4, T1–T3, and T1–Tx6 are common examples.

Parentheses are used to show the prolongation of a function through the change of bass. T1–T3 becomes T(1 3), and T1–Tx6 becomes T(1 x6), for example.

Contrapuntal prolongation – passing chord

Many change-of-bass prolongations involve a skip of a third in the bass, such as T(1 3). Just as in second-species counterpoint a melodic third from downbeat to downbeat invites the use of a passing tone, a melodic third in the bass between these two chords invites the use of a passing chord.

The bass note of a passing chord will fill in the third with stepwise motion. The melody will also often contain passing motion.

A function is typically prolonged by contrapuntal chords belonging to the function that precedes it in the standard cycle. T is prolonged by D, D by S, and S by T.

A passing chord that prolongs the above T(1 3) progression would then be a dominant chord (D precedes T) with scale-degree 2 in the bass (the passing tone between scale degrees 1 and 3): D2. In an interpreted functional bass, the D2 is placed within the parentheses, to show that it prolongs tonic rather than express its own function. It is also followed by a lower-case p to show that it functions as a passing prolongation. The whole progression is labeled T(1 D2p 3).

Contrapuntal prolongation – incomplete neighbor chord

In second-species counterpoint, variety could come by using a substitution in place of a passing tone. This leap of a fourth followed by step in the opposite direction still outlines a third from downbeat to downbeat, but offers a break from too much stepwise motion in the counterpoint.

In harmonic writing, the same effect is obtained by an incomplete neighbor chord. The bass follows the same pattern as the second-species counterpoint, and the function of the contrapuntal chord is the same as its passing-chord counterpart. Thus instead of a passing motion of T(1 D2p 3), a substitution pattern in the bass would produce T(1 D4i 3), with the i denoting an incomplete neighbor chord.

Contrapuntal prolongation – complete neighbor chord

Just as a neighbor tone in second- or third-species counterpoint could be used to ornament a single tone and return to it, a neighbor chord uses a neighbor-tone motion in the bass to prolong a function and return to the original bass pitch. The function of a neighbor chord follows the same principle as the passing or incomplete neighbor chord. Following are some examples of neighbor-chord prolongations:

• T(1 D7n 1)
• T(3 D4n 3)
• S(4 T3n 4)
• D(7 S6n 7)

Just as third-species counterpoint has a double neighbor figure, harmonies (especially T1) can be prolonged by two chords using a double-neighbor figure in the bass. Such a progression would be analyzed T(1 D(2 7)n 1).

Contrapuntal prolongation - divider and embellishing chords

In second-species counterpoint, an interval subdivision divided a large leap between downbeats into two smaller leaps. Likewise, a divider chord takes a large leap between bass notes in a change-of-bass prolongation (or a simple octave leap in the bass) and divides it into two smaller leaps.

Divider chords almost always prolong tonic function, and can do so using either subdominant or dominant dividers. The most common divider-chord prolongations are:

• T(1 D5d 1), where the bass ascends or descends an octave between T1 chords.
• T(1 S4d 1), where the bass ascends or descends an octave between T1 chords.
• T(1 S6d 3), dubbed the champagne progression by my undergraduate theory professor Gene Biringer, because it is "the progression you pull out when you want to impress a date." This progression is listed in the harmonic schemata resource, because it typically follows a unique voice-leading pattern.

In the case of the first two progressions, the same harmonic progression can occur without the bass changing register. In other words, the bass leaps from do to sol or fa, but returns to the original bass note. Instead of dividing a large leap, the bass note of the intervening chord looks like an embellishing tone from third species. (In third-species counterpoint, an embellishing tone ornaments another tone by leaping to another consonance (usually a third or fourth away) and returning to the original tone.) Thus, what would otherwise be a divider chord is instead an embellishing chord. Such a chord takes a postscript of e instead of d:

• T(1 D5e 1)
• T(1 S4e 1)

Subsidiary harmonic progressions

The last type of prolongation is not contrapuntal, but instead involves weak versions of the typical T–(S)–D–T progression. When such a progression fails to produce a proper cadence—i.e., ends with contrapuntal chords such as D7–T1 or D4–T3, or uses a "deceptive resolution" D5–Tx6 in place of the cadential D5–T1—the progression is called a subsidiary harmonic progression (the term comes from Edward Aldwell & Carl Schachter; Steven Laitz calls the same progression an embedded phrase model). It is "subsidiary" (or "embedded") because instead of occupying the whole phrase, it is subsidiary to (or embedded in) a larger progression. These subsidiary progressions always prolong tonic and are labeled with curly brackets {}.

For instance, consider the following possible harmonic progression for a phrase:

T1 S4 D4 T3 S4 D5 T1

The first progression through the T–S–D–T cycle does not produce a cadence when it returns to T. However, it cannot be said to be a contrapuntal prolongation because it follows the normal functional cycle perfectly. This is a subsidiary progression. When it is closed off in curly brackets to show its role prolonging tonic function, the phrase as a whole then shows a single, strong progression through the T–S–D–T cycle.

T{1 S4 D4 3} S4 D5 T1

It is important to use the curly brackets to show the difference between the subsidiary progression and the contrapuntal prolongation. They not only follow different harmonic patterns, but they sound different and originate with different concepts (prolonging tonic via voice-leading/counterpoint or via a weak harmonic progression).

Prolonging a progression

Occasionally, a contrapuntal chord is used not to prolong a single function, but to connect chords of different functions—in other words, to prolong a progression.

The most common occurrence is when a bass line moves down by step from do to sol, which is especially common in minor. The bass line do–te–le–sol is harmonized by T1 D7 S6 D5. While it may seem that the appropriate interpretation would be that S6 is a passing chord between the two dominants, that does not square with the sound of the progression—particularly when the S6 chord is a strong, chromatic subdominant chord. Instead, it makes more musical sense to hear the S6 as a functional subdominant leading to the cadential D5. The D7 chord, then, is simply a passing chord that connects T1 with S6.

To notate this by hand, draw and arrow between T1 and S6, and place D7p on top of the arrow. When entering the functional bass into notation software, it is fine to notate the progression T1 D7p S6 D5. The meaning will be understood. However, when analyzing by hand, the arrow makes the interpretation clearer, and therefore should be used.